Using Northwest Corner for Transportation Problem
Solving Transportation Problems with the Northwest Corner Method
Efficient resource allocation is crucial in logistics, supply chain management, and operations planning. One of the most common models to handle such problems is the transportation problem—a type of linear programming that aims to minimize the cost of shipping goods from multiple sources to multiple destinations (Prifti et al., 2020).
To find a solution, various methods can be applied. Among them, the Northwest Corner Method (NWC) stands out as a simple and intuitive starting approach. The method may not be the most optimal, but it provides a feasible solution that serves as a base for further optimization using more advanced techniques like MODI or Stepping Stone.
What is the Northwest Corner Method?
The Northwest Corner Method is a basic initial solution algorithm used to fill the transportation table. It’s called “northwest” because it starts at the top-left corner of the matrix and proceeds from there following a structured rule (Ahyaningsih et al., 2023).
This method ignores shipping costs at the beginning and focuses only on satisfying supply and demand constraints.
How Does it Work?
Step 1: Start at the top-left (northwest) cell
- Begin with the cell located in the first row and first column.
Step 2: Allocate as much as possible
- Allocate as many units as possible to that cell, either the supply available or the demand needed. Choose the smaller number.
- Subtract the allocated units from both the supply and demand.
Step 3: Move to the next cell
- If the supply for a row is used up, move down to the next row.
- If the demand for a column is fulfilled, move right to the next column
- Move diagonally if both supply and demand are zero.
Step 4: Repeat until all supply and demand are met
- Continue the process until the entire transportation table is filled with feasible allocations.
Step 5: Calculate the total shipping cost
- For every cell, multiply the shipping cost by the allocated number.
- You get the total shipping cost by summing up the product of units and shipping cost in each cell.
Example Question
Question:
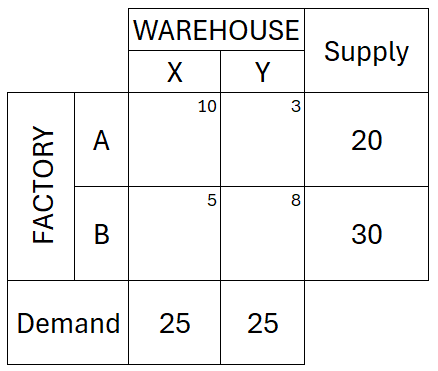
Let's say you have 2 factories (sources, denoted as F) and 2 warehouses (destinations, denoted as W).
The supply from Factory A is 20 units. Meanwhile, the supply from Factory B is 30 units.
On the other hand, both Warehouse X and Y have a demand of 25 units each.
The transportation costs are as follows:
- Factory A to Warehouse X = $10
- FA to WY = $3
- Factory B to Warehouse X = $5
- FB to WY = $8
Refer to figure 1 for an illustration of the question.
How many units must be allocated for each transportation route? What will be the total transportation cost for it? (Use the Northwest Corner Method.)
Solution:
To solve this question, follow the steps explained above. Hence, the solution will be as such:
Step 1: Start at the top-left cell (from Factory A to Warehouse X). Here, there are two things to take note of. The demand from Warehouse X is 25. However, the supply from Factory A is 20. So, the maximum allocation in that cell will be 20 units.
Step 2: Factory A reaches its limit. So, move down to cell B-X (from Factory B to Warehouse X). Since the remaining demand for Warehouse X is 5 units, this cell will be allocated 5 units.
Step 3: The demand for Warehouse X has been met. So, move to cell B-Y (from Factory B to Warehouse Y). Allocate the remaining supply of Factory B to this cell. Hence, this cell will have 25 units.
Figure 2 gives an overview of the solution.
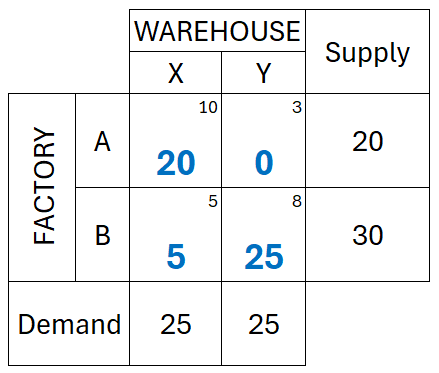
After finding out the allocations for each route. The total transportation cost will be calculated as follows:
(20 x 10) + (5 x 5) + (0 x 3) + (25 x 8) = 200 + 25 + 200 = $425
So, the total transportation cost with the given allocation will be $425.
When Should This Method Be Used?
The Northwest Corner Method is ideal when:
- You need a quick initial solution
- Testing out a transportation model
- Shipping cost is not a major concern at the early stage
- It's part of a larger algorithmic solution (e.g., input to MODI)
However, it is important to note that this method ignores cost. This means that it often leads to non-optimal solutions (Kalaivani & Visalakshidevi, 2024). That is why many analysts use it as a first step and not as the final decision.
Strengths and Weaknesses
Advantages:
- Simple and fast
- Always gives a feasible solution
- Easy to understand, even for beginners
Disadvantages:
- Ignores transportation costs
- Rarely gives the optimal solution
- May lead to higher total cost
Final Thoughts
The Northwest Corner Method is an essential tool in the operations research toolkit. While it doesn't give the most efficient shipping plan, it lays the groundwork for more refined methods to improve upon.
Once you master the Northwest Corner Method, the next step is to explore the Least Cost Method, Vogel Approximation Method, or the MODI Method to bring your transportation plan closer to optimal.
References
Ahyaningsih, F., Nasution, H., & Sitanggang, E. A. (2023). Implementation of North West Corner (NWC) Method and Modified Distribution (MODI) method in optimizing fish distribution costs in CV. horizon group sibolga. In Sciendo eBooks (pp. 357–367). https://doi.org/10.2478/9788367405195-048
Kalaivani, N., & Visalakshidevi, E. (2024). A generalized novel approach to transportation problem using multi partite-graph method. Measurement Sensors, 33, 101060. https://doi.org/10.1016/j.measen.2024.101060
Prifti, V., Dervishi, I., Dhoska, K., Markja, I., & Pramono, A. (2020). Minimization of transport costs in an industrial company through linear programming. IOP Conference Series Materials Science and Engineering, 909(1), 012040. https://doi.org/10.1088/1757-899x/909/1/012040
SGD's 4 : Quality Education


Comments :