Minimizing Transportation Costs with the Least Cost Method

In logistics and supply chain management, cost efficiency is just as important as meeting demand. That’s why solving transportation problems isn’t only about finding a feasible solution—it’s about finding a low-cost one. After using simple methods like the Northwest Corner Method (NWC) to get a starting solution, the Least Cost Method (LCM) offers a smarter way to build an initial plan that considers cost right from the start.

This article explains how the Least Cost Method works, when to use it, and how it helps bring businesses closer to optimal transportation plans.

What is the Least Cost Method?

The Least Cost Method is a technique used to solve transportation problems by starting with the lowest possible cost (Nugraha et al., 2023). Unlike NWC, which ignores cost in its early steps, LCM builds the allocation by selecting cells with the smallest unit cost first, while still satisfying supply and demand constraints.

Its goal is to generate a better initial basic feasible solution (IBFS)—one that’s closer to the optimal solution and more efficient from the beginning.

Step-by-Step: How the Least Cost Method Works

Step 1: Identify the cell with the lowest cost

  • Look across the entire cost matrix.
  • Choose the cell with the lowest shipping cost.

Step 2: Allocate as much as possible to that cell

  • Allocate the maximum number within the limit of the demand or supply to that cell.
  • Subtract the allocation from both row supply and column demand.

Step 3: Cross out the row or column that has been fulfilled

  • If the demand has been fulfilled, then the rest of the cells in that column will be allocated 0 units.
  • If the supply has been fulfilled, then the rest of the cells in that row will be allocated 0 units.

Step 4: Repeat the process

  • Continue selecting the next lowest-cost cell from the remaining options.
  • Repeat allocation and crossing out until all supply and demand values are satisfied.

Step 5: Calculate the total shipping cost

  • The total shipping cost can be found by summing up the product of units and shipping cost in each cell.

Example Question

Question:

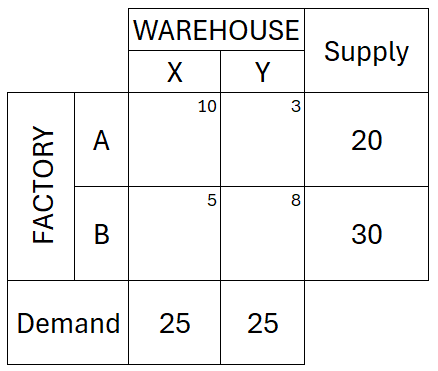
Let's say you have 2 factories (sources, denoted as F) and 2 warehouses (destinations, denoted as W).

The supply from Factory A is 20 units. Meanwhile, the supply from Factory B is 30 units.

On the other hand, both Warehouse X and Y have a demand of 25 units each.

The transportation costs are as follows:

  • Factory A to Warehouse X = $10
  • FA to WY = $3
  • Factory B to Warehouse X = $5
  • FB to WY = $8

Refer to figure 1 for an illustration of the question.

Example Question for Least Cost Method
Figure 1. Example Question for Least Cost Method

Solution:

Step 1: Find the lowest cost

  • The lowest cost is at cell AY with only a $3 shipping cost.
  • It has a limit of 20 units for supply and 25 units for demand.
  • So, allocate 20 units in that cell.
  • A's supply is now 0, so cross out the rest of row A.

Step 2: Next lowest cost

  • The next lowest cost is at cell BX, costing $5.
  • It has a limit of 30 units for supply and 25 units for demand.
  • So, allocate 25 units in that cell.
  • X's demand is now 0, so cross out the rest of column X.

Step 3: The last cell

  • The only cell left to be filled out is cell BY, costing $8.
  • Fill it out with the remaining 5 units.
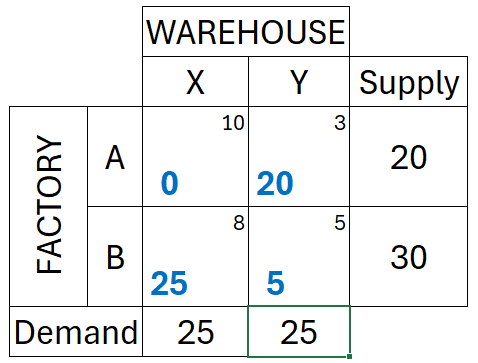
Answer using least cost method
Figure 2. Example Question's Answer Using the Least Cost Method

Step 4: Total shipping cost

The total shipping cost is the sum of the product of the allocated units by the shipping cost.

(20 x 3) + (25 x 5) + (5 x 8) = $225

Strengths and Weaknesses

Advantages:

  • Considers cost
  • Provides a closer approximation to the optimal solution
  • Works for most real-world transport model

Disadvantages:

  • Still no guarantee that the result is optimal
  • Slightly more complex than the Northwest Corner Method
  • Needs tie-breaking if multiple lowest cost exist

Final Thoughts

The Least Cost Method is a practical and powerful tool in solving transportation problems. It builds on the strengths of simpler methods like NWC, but goes a step further by introducing cost-awareness into the equation. While it may not always give the absolute best answer, it gets you much closer to the ideal solution—saving time, money, and resources.

References

Nugraha, I., Winursito, Y. C., & Sari, T. P. (2023). Shipping cost optimization using least cost and stepping stone method at the Xender brand sandal factory. Biomedical and Mechanical Engineering Journal (BIOMEJ), 3(1), 36–42. https://doi.org/10.33005/biomej.v3i1.74

SGD's 4 : Quality Education